Ants Simulation
Abstract
Our program simulates the behavior of ants trying to find the shortest way to a food source starting from their nest.
Therefore, we have used the ant colony optimization algorithm based on the principle that ants drop a certain amount of pheromone, while they return to their nest after having found a food source.
This makes other ants follow their path.
On a long timescale, this leads to emergence of optimal paths because, in average, the shortest way is the most used one. In our simulation, a two-dimensional map containing a nest and several randomly placed food sources can be generated.
The ants start searching for food, performing a random walk. When an ant finds a food source, it walks back the exact way it came, spreading pheromone. Ants starting from the nest now try to follow the pheromone.
This makes other ants follow their path.
On a long timescale, this leads to emergence of optimal paths because, in average, the shortest way is the most used one. In our simulation, a two-dimensional map containing a nest and several randomly placed food sources can be generated.
The ants start searching for food, performing a random walk. When an ant finds a food source, it walks back the exact way it came, spreading pheromone. Ants starting from the nest now try to follow the pheromone.
Simulation
Key
Map points:
The pheromone concentration is visualized by colors between yellow (low) and red (high). The food rate shows, how much food is currently collected per second.
The simulation speed can be adjusted via the speed slider, which sets the number of calculation steps (equates to ant steps) per second.
- brown: border
- white: empty
- green: food source
- gray: nest
- black: seekers (and unsuccessful seekers)
- blue: followers
- green: returners
The pheromone concentration is visualized by colors between yellow (low) and red (high). The food rate shows, how much food is currently collected per second.
The simulation speed can be adjusted via the speed slider, which sets the number of calculation steps (equates to ant steps) per second.
Map points
Every map point contains two attributes: its type (border, nest, food, empty) and its pheromone concentration.
The map we use is created by placing N food sources on the 150 × 100 points map randomly. The nest is set on a map point which is located somewhere in the center of the map. All points on the edges are made border points, which stops the ants from leaving the map.
In the simulation, it is possible to set the type of map points to any of the types mentioned.
The map we use is created by placing N food sources on the 150 × 100 points map randomly. The nest is set on a map point which is located somewhere in the center of the map. All points on the edges are made border points, which stops the ants from leaving the map.
In the simulation, it is possible to set the type of map points to any of the types mentioned.
Ant types and behavior
We consider four different ant states: seeker, follower returner and returner2. Depending on the pheromone concentration around the nest, the ants spawn as followers or seekers.
Therefore, we generate a random integer.
If the pheromone concentration of one map point around the nest is higher than this integer, the ant becomes a follower, otherwise it becomes a seeker.
If the pheromone concentration of one map point around the nest is higher than this integer, the ant becomes a follower, otherwise it becomes a seeker.
- Seeker: A seeker is performing a random walk. In every time step, it chooses one of the three points in front of it and saves every step it does in an array list (which thus contains the whole way). If the ant reaches a food source, it turns into a returner. A seeker also counts its steps and, after not finding food for 450 steps, unsuccessfully returns to the nest as a returner2.
- Follower: A follower can only move to points, whose distance to the nest is greater than the current position of the ant. The possible points to which the ant could move in the next step are given probabilities to move there. These probabilities are determined by the pheromone concentrations on the points. If the sum of the pheromone concentration in the map points around the ant is very low (that means the ant lost the path it was following), the ant changes its state to seeker. When a follower finds food it turns into a returner.
- Returner: A returner is moving to the nest on the same way it came, spreading pheromone. The amount of pheromone dropped in every step can be varied (pheromone drop).
- Returner2: A returner2 moves back to the nest without spreading pheromone.
Pheromone
When a returner drops pheromone, it drops a certain amount of pheromone in the center of its location and some fraction of that amount in a circle around the center.
The pheromone drop amount can be set inside the simulation.
In every time step, the pheromone concentration of every map point decreases according to the following formula (depending on a constant k):
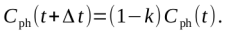
The pheromone decay constant k can be varied inside the simulation as well.
In every time step, the pheromone concentration of every map point decreases according to the following formula (depending on a constant k):
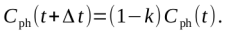
The pheromone decay constant k can be varied inside the simulation as well.
Download
You can download an executable JAR file including the simulation and the Java source code from here: